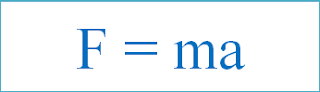Leaning Online

Here we discuss about the difference between Expense Recognition Principle and Matching Principle and both of these principles are included in Generally Accepted Accounting Principles (GAAP). Expense Recognition Principle states that expenses should be recorded when incurred whether the cash is paid or not. Matching Principles states that all the expenses incurred for generating revenue must be matched with that particular revenue. Because in Expense Recognition Principle we record the expenses when these are incurred whether the cash is paid or not i.e., it also involves a Credit Transaction alongwith a Cash Transaction, therefore, we focus only on the recording of expenses. For Example, Rent paid for Rs.5000 on Account are recognized as expense whether the cash is paid or not. While in Matching Principles, we set off the revenues with the expenses incurred for earning that revenue. For Example, On 1 st March, 2017 Rent Paid For Rs.5000 on Account...

Here we need to prove that a = F / m or there is an inverse relationship between acceleration (a) and mass (m) of the body if a force is applied on the body. We already know that according To Newton’s Second Law of Motion : F = ma  So from this equation, we get: a = F / m Now, here is the proof that: a = F / m Suppose a body of Mass 10 kg is moving by applying a Force of 30 N, then what is the acceleration of the body? We know that: F = ma a = F / m a = 30 / 10 = 3 Left Hand Side = a = 3m/s 2 Now taking Right Hand Side, we get: Right Hand Side = F / a Right Hand Side = 30 / 10 Right Hand Side = 3 (Newton / Kg) Hence a = F / m Hence we have proved that there is an inverse relationship between a and m of the body according to Newton’s Second Law of Motion .

Physics Questions Answers This is the equation of Newton’s Second Law of Motion . Here F is the force applied on the body, m is the mass of the body which is inversely proportional to the applied force and a is the acceleration produced in the body by the force and it is directly proportional to the applied force. Examples of Newton’s Second Law of Motion Example No. 1 Suppose a body of Mass 20 kg is moving by applying a Force of 40 N, then what is the acceleration of the body? We know that: F = ma a = F / m a = 40 / 20 =2 a = 2m/s 2 Hence Acceleration is 2ms -2 and it is produced in the body when a force of 40 N is applied on the mass of 20 Kg. Example No. 2 Suppose a body of Mass 20 kg is moving by applying a Force. The body is moving with an acceleration of 2ms -2 , then what Force (F) was applied on body? We know that: F = ma F = 20 x 2 F = 40 N Hence Force is 40 N and it is a...

Before written down the Kinetic Energy Formula, we know firstly, what is Energy? And What is Kinetic Energy? And then we get the formula after considering an example. An Energy is the ability to do the work. The energy is stored in a body and when the work is done on it, the body performs a work due to its energy. Energy is found in many forms like Nuclear, Electrical, Magnetic, Chemical, Mechanical and so on. Now we are in a position to define Kinetic Energy: Kinetic Energy Definition “Kinetic Energy is stored by a body due to its Motion” Kinetic Energy Example Let suppose, a body having mass m is moving with an initial velocity V i ,  and a constant force F is applied on the body to stop it, then according to Newton’s Second Law of Motion , the acceleration is given as: a = - F / m As body comes to rest after converting some distance d, its velocity V f is zero, and according to Second Motion of Equation or Ki...

Kinematic Equations represent the motions of a body moving with constant velocity or uniform acceleration. When the body is moving with constant velocity or velocity increases with constant rate, then the body is moving with uniform positive acceleration. At this point, its initial velocity is zero and hence its acceleration is also zero. There is no change in velocity, so body is moving with uniform acceleration. These Kinematic Equations are: V f = v i + at     (i) S = V i   t + ½ at 2    (ii) V 2 f = V 2 i + 2aS   (iii) By utilizing these equations, we can find the values of V f , S, t, a and V i . Example, suppose a car is moving with a velocity of 300 km hr -1 after a distance of .45 km at constant acceleration. Find the acceleration. Here Vi = 0 , Vf = 300 km hr -1 = 300 x 1000/ 1/3600 =  300 / 3.6 = 83.33 ms -1 S = 0.45km = .45 x 1000 = 450m ...

Here we discuss about Oligopoly. Oligopoly Definition We can define Oligopoly as: “It is the market model in which there are very few sellers producing either homogenous (Similar) or differentiated products and where the decision making powers of the firm depend on the expected reactions of other market firms and also the entry to the market is difficult or blocked by big firms”. Examples of Oligopoly Market Model include Automobiles Companies, Software House Companies, Air-Lines, Oil Producing and Exporting Countries. Features or Characteristics of Oligopoly 1. Few Sellers It is a market situation in which the number of firms or sellers is very few. They produce similar or differentiated products. 2. Interdependence In this market model, since there is good substitute of the products, so the policies of one producer significantly affect the decisions making powers of other sellers. One can see Higher Cross Elasticity of Deman...

Here we study about Hooke’s Law. Hooke’s Law states that: “There is direct relationship between Stress and Strain till there is constant value of E”. Hooke’s Law Equation  can be written in the mathematical form as: Stress / Strain = Constant (E) Here Stress is the force applied to change the volume or shape of the body. Strain is the change in shape or change in volume of the body after being a force applied on the body. E is called the Modulus of Elasticity or Co-Efficient of Elasticity. If this constant value exits between stress and strain, then the law of Hooke holds good. So, now you will be able to learn about Hooke’s Law.

Here we discuss about Newton’s third law of motion. You may also be interested in Newton’s First Law and Newton’s Second Law of Motion Newton’s 3rd Law states that: “Actions and reactions are Equal in magnitude but in opposite direction”. This law tells us the universal truth that all the bodies in the environments show pair of action-reaction forces that are equal in magnitude but opposite in direction. If an force is acted on a body and at the same time an reaction of equal magnitude act on this body in opposite direction, then we can write Newton’s Third Law in the form of an equation as shown below: F A = -F B Here F A is the Action that is exerted by body A on body B and as the result an reaction of force (-F B ) of equal in magnitude acts on body A from the body B. We should not miss up Newton’s First Law and Newton’s Law of Motion , because when we exert the force on the ground, then there is reaction of equal mag...